MATLAB / Octave Tutorial : Generating various signals

Chapter 4: Generating various signals

Part 1: Generating Simple Signals

Welcome all to a whole new chapter of learning MATLAB / Octave. I know its been a long time since we have hoisted any new chapter. So, lets start with something interesting. In this chapter we will learn how to create simple signal forms like sine, cosine and square waves.

Let's start with some math first. We'll be defining a function as follows:

y=sin(2πft)

(1)

Where, f=Frequecy of the signal

and t= time range

In MATLAB / Octave, sin takes argument in radians. So, we have to convert frequency in Hertz to radians per second.

Now we write the following lines of code to generate a sine signal of 100Hz.

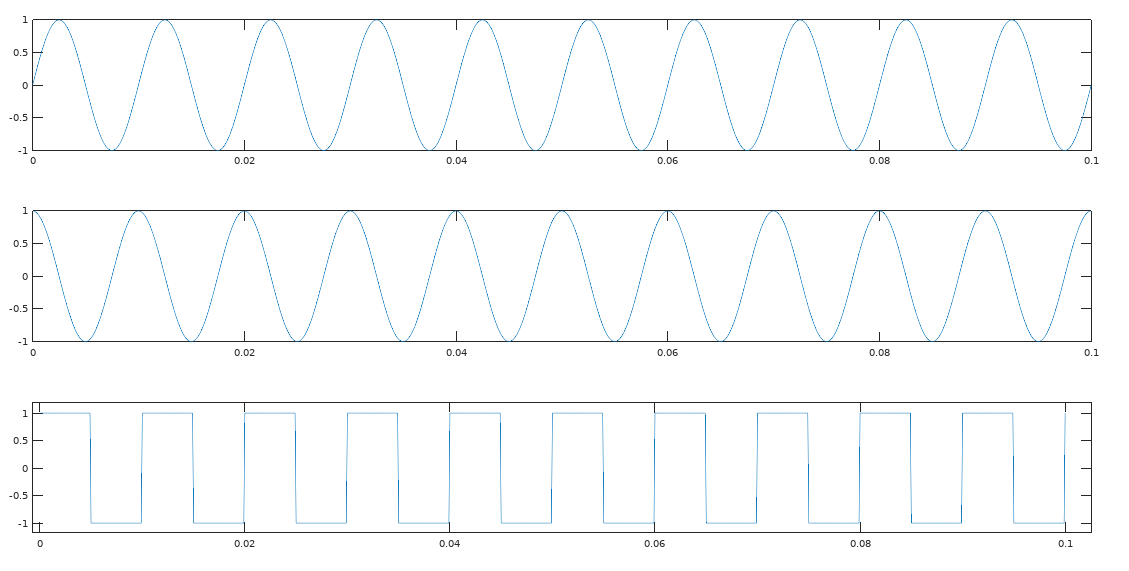
If we plot the signal, it will look something like this:

Quite bizzare, right! Yes, that’s what a 100Hz signal looks like in a 0 to 1s scale. Now, lets analyse each line of code in detail.

f=100	This is the frequency of the signal
t=0 : 0.00001 : 1	This line is very important. This line defines the time range of the signal, i.e., 0 to 1 second, with a time accuracy of 0.00001s. Now, why did I choose this value? This value is chosen as to how much detailed values we want to have for each point in the graph. A less value means the points in the graph will be closer and the graph will be smoother and a bigger value means the points will be far from each other resulting a less smooth graph.
y= sin(2*pi*f*t)	This is same as eqn 1 above.

This is the first 2 cycles of the above graph:

Now, let’s decrease the time accuracy. Now we take, t=0 : 0.001 : 1 and lets see the result.

Hence, you see that the graph is not at all smooth as that was above. Lowering the accuracy will result in worse results (you can try it out yourselves!).

Generating cosine signals is same. Instead of sin you use cos like so:

y=cos(2*pi*f*t)

and you will get your results.

Now, let’s learn a bit about generating square waves. Generating square waves is same as above. The only additional argument is the duty cycle given by the formula:

 

on time duty cycle = --------------------------                                                  on time + off time

(2)

Command for generating square wave is:

                                                 square(2*pi*f*t)

This function is overloaded with another argument as shown below:

                                             square(2*pi*f*t, D)

where, D is the Duty cycle.

Let, a square pulse is ON / HIGH for 0.5 s and OFF / LOW for 0.2s. So, the duty cycle will be

                                                                                                         0.5

      D = ------------ = 0.714

0.5+0.2

By default, the duty cycle is 0.5.

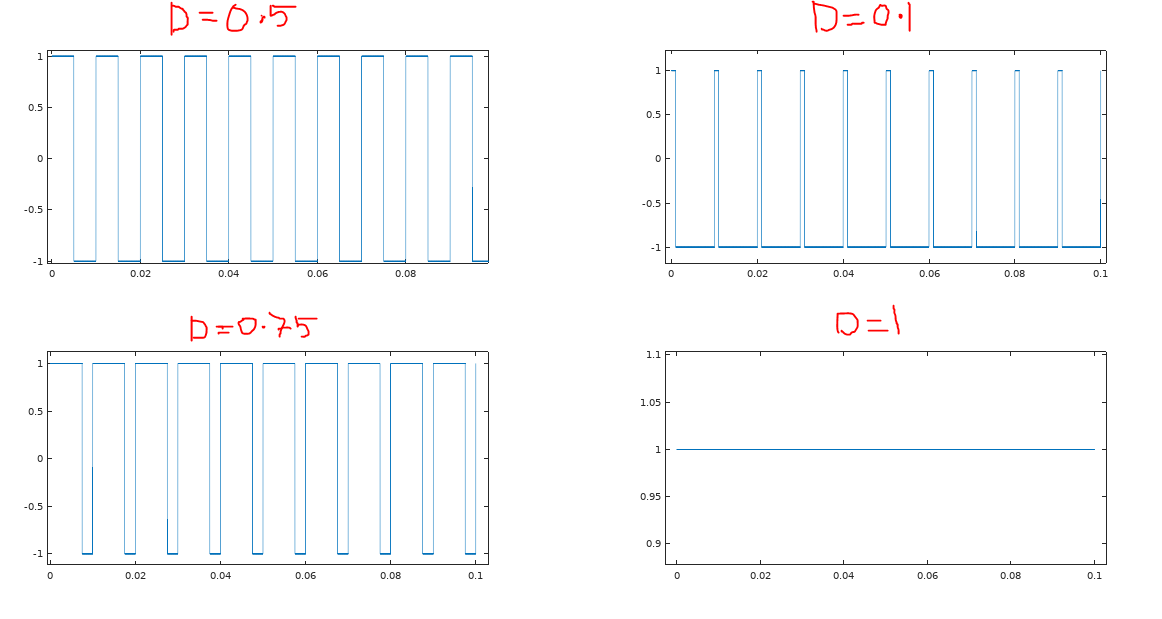
Lets see what various square waves with different duty cycles look like:

You can try with different duty cycles as per your requirements and see the various wave forms.